高卒でもわかる機械学習 (6) 誤差逆伝播法 その2

今回書くこと

前回、多層パーセプトロンの重み更新の理論として、誤差逆伝播法の考え方の概要を、数式を使って説明しました。
しかし出てきた数式が出力層付近のみの式だったので、今回はすべての層に一般化した更新式を導きます。

デルタの定義

ここで、今回とても重要になる定義をします。
任意の第 $l$ 層 $k$ 番目のユニットの重み付き和を $u_k^{(l)}$ のように書くと定義しましたが、この $u_k^{(l)}$ で誤差関数 $E$ を偏微分したものを $\delta^{(l)}_k$ とおきます。

$\delta_k^{(l)} = \frac{\partial E}{\partial u_{k}^{(l)}}$

上記はすべての出力ユニット¹でそれぞれ定義されることにご注意ください。
例： $\delta_m^{(l+1)} = \frac{\partial E}{\partial u_{m}^{(l+1)}}$ 、 $\delta_n^{(L)} = \frac{\partial E}{\partial u_{n}^{(L)}}$
なお、この値の意味は…と深く考える必要はありません。
後の計算式がわかりやすくなるように定義したものです。

$\delta$ はギリシャ文字の $\Delta$ （デルタ）の小文字です。
以下、これらの値をそのまま「デルタ」と呼ぶことにします。²

デルタを使って出力層の更新式を表す

出力層にひもづく重みの更新式は前回導きましたが、これをデルタを使った式で改めて導き直してみます。
まず出力層（第 $L$ 層） $i$ 番目のユニット出力値の式は下記ですね。

$o_i^{(L)} = f(u_i^{(L)})$

$u_i^{(L)} = w_{i, 0}^{(L)} + w_{i, 1}^{(L)} o_1^{(L-1)} + w_{i, 2}^{(L)} o_2^{(L-1)} + \cdots$

勾配降下法による重み更新式はこうでした。（第 $L$ 層 $i$ 番目ユニットの $j$ 番目の重み）

$w_{i, j}^{(L)} \gets w_{i, j}^{(L)} - \rho \frac{\partial E}{\partial w_{i, j}^{(L)}}$

上記の $\frac{\partial E}{\partial w_{i, j}^{(L)}}$ について

$\begin{align*} \frac{\partial E}{\partial w_{i, j}^{(L)}} & = \frac{\partial E}{\partial u_i^{(L)}} \frac{\partial u_i^{(L)}}{\partial w_{i, j}^{(L)}} \\ & = \delta_i^{(L)} o_j^{(L-1)} \end{align*}$

となります。
よって出力層の重みの更新式は

$w_{i, j}^{(L)} \gets w_{i, j}^{(L)} - \rho \delta_i^{(L)} o_j^{(L-1)}$

と表せます。
随分シンプルな式になりました。

ところで、出力層のデルタはどんな式で表せるでしょうか。展開してみます。

$\begin{align*} \delta_i^{(L)} & = \frac{\partial E}{\partial u_i^{(L)}} \\ & = \frac{\partial E}{\partial o_i^{(L)}} \frac{\partial o_i^{(L)}}{\partial u_i^{(L)}} \\ & = \left( o_i^{(L)} - t_i \right) f'(u_i^{(L)}) \end{align*}$

項ごとの変形は前回やったことと同じですので、意味がわからない場合は前回の記事を参照してみてください。

デルタを使って出力層以外の更新式を表す

出力層以外の任意の第 $l$ 層について考えてみます。

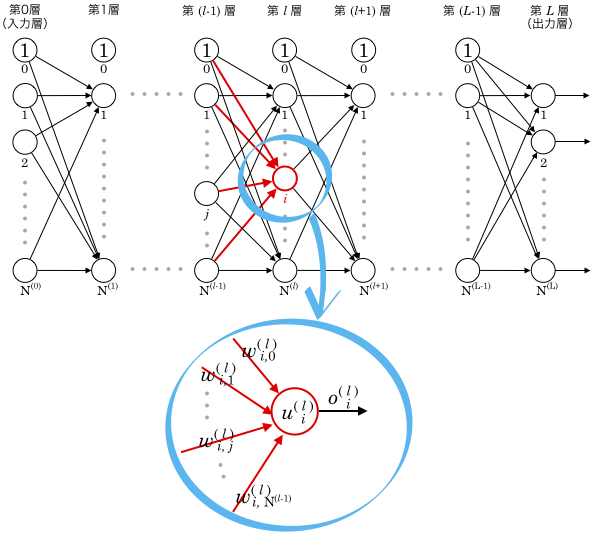
mlp_name

第 $l$ 層の $i$ 番目のユニットの式は下記のようになります。

$o_i^{(l)} = f(u_i^{(l)})$

$u_i^{(l)} = w_{i, 0}^{(l)} + w_{i, 1}^{(l)} o_1^{(l-1)} + w_{i, 2}^{(l)} o_2^{(l-1)} + \cdots$

勾配降下法による重み更新式はこうですね。（第 $l$ 層 $i$ 番目ユニットの $j$ 番目の重み）

$w_{i, j}^{(l)} \gets w_{i, j}^{(l)} - \rho \frac{\partial E}{\partial w_{i, j}^{(l)}}$

上記の $\frac{\partial E}{\partial w_{i, j}^{(l)}}$ は

$\begin{align*} \frac{\partial E}{\partial w_{i, j}^{(l)}} & = \frac{\partial E}{\partial u_i^{(l)}} \frac{\partial u_i^{(l)}}{\partial w_{i, j}^{(l)}} \\ & = \delta_i^{(l)} o_j^{(l-1)} \end{align*}$

と変形できるので、更新式は下記のようになります。

$w_{i, j}^{(l)} \gets w_{i, j}^{(l)} - \rho \delta_i^{(l)} o_j^{(l-1)}$

出力層の場合とほとんど同じ式になっていることがわかるでしょうか？

ただし、デルタを展開すると、出力層とはだいぶ違う式になります。
展開してみましょう。下記の部分までは同じです。

$\begin{align*} \delta_i^{(l)} & = \frac{\partial E}{\partial u_i^{(l)}} \\ & = \frac{\partial E}{\partial o_i^{(l)}} \frac{\partial o_i^{(l)}}{\partial u_i^{(l)}} \end{align*}$

上式の最終行第1項は、下記のように展開できます。
（前回名付けた、偏微分の公式の「難しい方」を使っています。）

$\begin{align*} \frac{\partial E}{\partial o_i^{(l)}} & = \sum_k \frac{\partial E}{\partial u_k^{(l+1)}} \frac{\partial u_k^{(l+1)}}{\partial o_i^{(l)}} \\ & = \sum_k \delta_k^{(l+1)} w_{k,i}^{(l+1)} \end{align*}$

式中に第 $(l+1)$ 層のデルタが出現しました。
前出のデルタ展開式に上記を当てはめます。

$\begin{align*} \delta_i^{(l)} & = \frac{\partial E}{\partial o_i^{(l)}} \frac{\partial o_i^{(l)}}{\partial u_i^{(l)}} \\ & = \sum_k \delta_k^{(l+1)} w_{k,i}^{(l+1)} f'(u_i^{(l)}) \end{align*}$

第 $l$ 層のデルタを表現するのに、第 $(l+1)$ 層のデルタを使うことができました。
これは、下記のことを表しています。

上の層の更新式を計算すると、その計算結果の一部を下の層の更新式に使い回すことができる
ただし、この式は出力層では使えない

1つ目については、前回も触れた内容ですね。
2つ目については、層番号は出力層の $L$ が最大で、第 $(L+1)$ 層というのはないからです。
つまりデルタの式は、出力層（ $l = L$ ）とそれ以外（ $l < L$ ）で違うということです。
出力層のデルタは、この記事の前半で式展開しましたね。

まとめます。

多層パーセプトロンの重み更新アルゴリズム

多層パーセプトロンの第 $l$ 層 $i$ 番目ユニットの $j$ 番目の重みの更新式は下記で表せます。

$w_{i, j}^{(l)} \gets w_{i, j}^{(l)} - \rho \delta_i^{(l)} o_j^{(l-1)}$

ただし、

$\delta_i^{(l)} = \begin{cases} \left( o_i^{(l)} - t_i \right) f'(u_i^{(l)}) & (l = L) \\ \sum_k \delta_k^{(l+1)} w_{k,i}^{(l+1)} f'(u_i^{(l)}) & (l < L) \end{cases}$