高卒でもわかる機械学習 (3) 多層パーセプトロン

XOR問題：単純パーセプトロンの限界

単純パーセプトロンの学習によって論理演算（ANDやORなど）の役割を果たす識別器を作ることを考えます。
真 = 1, 偽 = 0 とおき、 $x_1$ , $x_2$ それぞれでいずれかを入力します。
パーセプトロンを通過した結果、それらを論理演算した値（0または1）が出力されるようにします。

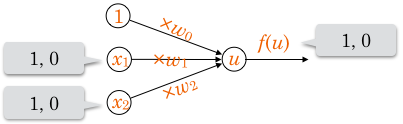
論理演算パーセプトロン

0か1の出力なので、活性化関数 $f$ として単位ステップ関数を利用します。

$f(u) = \begin{cases} 1 & (u \geq 0) \\ 0 & (u < 0) \end{cases}$

単純パーセプトロンにおける重みベクトルの学習手順は前回説明したとおりですので、以下、学習によって具体的にどのような重みになってほしいか？という観点で話を進めます。
以下のようなアプローチで考察ができるのは2次元（入力が2つ）ならではです。

OR（論理和）

まず、ORの役割を果たす単純パーセプトロンについて考えます。
OR の定義は下表のような感じですよね。

$x_1$	$x_2$	$x_1$ OR $x_2$
1	1	1
1	0	1
0	1	1
0	0	0

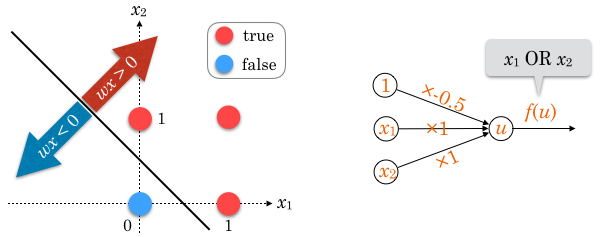
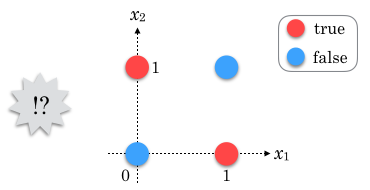
入力値 $x_1, x_2$ をグラフにプロットし、出力値の境界に適当な直線を引いてみると、例えば傾きが-1で切片が0.5、つまり $x_2 = -x_1 + 0.5$ の直線で分割できることがわかります（下図参照）。¹
移項して $w_0 + w_1x_1 + w_2x_2 = 0$ の形に直すと、 $-0.5 + x_1 + x_2 = 0$ です。
左辺の $x_1$ , $x_2$ に図中の赤い点の値を代入すると $-0.5 + x_1 + x_2 > 0$ 、青い点の値を代入すると $-0.5 + x_1 + x_2 < 0$ となり、この $-0.5 + x_1 + x_2$ が識別関数として機能していることがわかります。
つまり、学習の結果重みベクトルが例えば $\bm{w} = \left( \begin{array}{c} -0.5 \\ 1 \\ 1 \end{array} \right)$ になれば、この単純パーセプトロンは OR の役割を果たします。
なお、 $w_0$ : $w_1$ : $w_2$ の比率がだいたいそれに近ければ同じ出力をしたりします。

ORグラフ

AND（論理積）

AND は下表です。

$x_1$	$x_2$	$x_1$ AND $x_2$
1	1	1
1	0	0
0	1	0
0	0	0

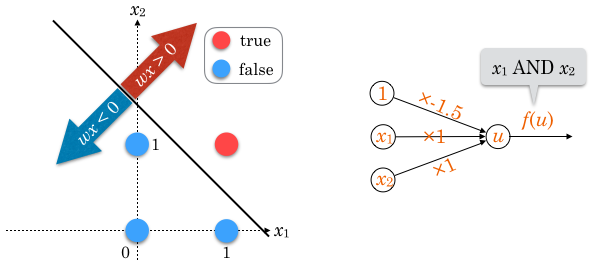
入力値 $x_1, x_2$ をグラフにプロットし、出力値の境界に直線を引いてみると、例えば $x_2 = -x_1 + 1.5$ で分割でき、これを OR と同じように整理すると $\bm{w} = \left( \begin{array}{c} -1.5 \\ 1 \\ 1 \end{array} \right)$ です。

ANDグラフ

NAND（否定論理積）

NAND（つまり NOT AND）は下表です。

$x_1$	$x_2$	$x_1$ NAND $x_2$
1	1	0
1	0	1
0	1	1
0	0	1

当然ですが、演算結果がANDと反転しています。
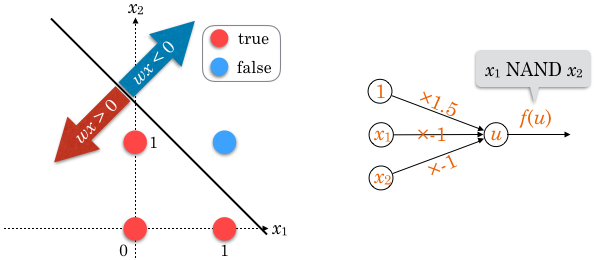
AND と同じ直線で分離できるのですが、直線で分離された両エリアの不等号が逆になります。
不等式の不等号を逆にするためには、両辺に -1 をかければいいですね。
よって、AND の重みの正負を逆転させた $\bm{w} = \left( \begin{array}{c} 1.5 \\ -1 \\ -1 \end{array} \right)$ が適切な重みの一例です。

NANDグラフ

XOR（排他的論理和）

XORは下表です。

$x_1$	$x_2$	$x_1$ XOR $x_2$
1	1	0
1	0	1
0	1	1
0	0	0

これまでとちょっと様子が違います。
グラフを見るとわかるように、4点を直線で分割することができません。
つまりこれは線形識別不可能な問題であり、単純パーセプトロンでは解決することができないのです。

XORグラフ

多層パーセプトロン

$x_1$ XOR $x_2$ は、「 $x_1$ , $x_2$ どちらかは真だが、『両方が真』ではない」時に真となります。
つまりこのように表現できます。

XORの式を分解

OR、AND、NAND を使って表現できました。
この3つの演算子は単純パーセプトロンで作成できるので、それらをつなぎ合わせることで結果的に XOR の役割を果たす識別器が作れます。

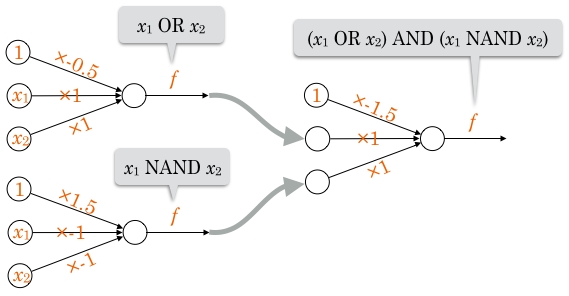
XORをパーセプトロンで

まとめた絵にするとこうです。

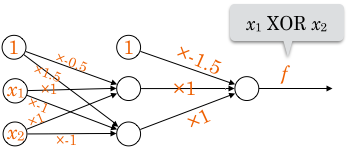
XORをパーセプトロンで

「あるユニットの出力を別のユニットの入力として使う」という構造を作ったことで、線形識別不可能な問題を解くことができました。²
これが多層パーセプトロンです。³
この例では、真ん中の2ユニットの出力が右のユニットの入力として使われています。

一般に、つなぎ合わせるユニットの数は問題によって様々ですが、非常に多くのユニットを結合させて利用することも多いです。

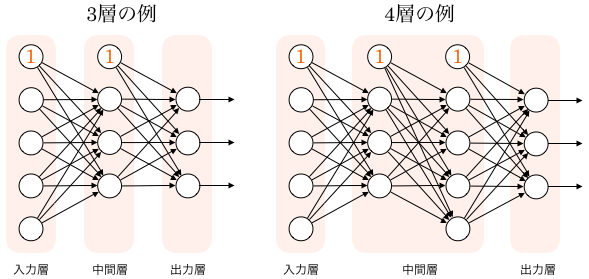
3層と4層の多層パーセプトロン

このように、ユニットが層状になっていることから多層パーセプトロンと言います。
上図で、一番左の層を入力層、一番右の層を出力層、それ以外の層を中間層または隠れ層と呼びます。
この図では出力層にユニットが複数ありますね。その意義の一例は後の項で述べます。

XORの例は、「多層にすることによって、【重みの値を適切に学習できさえすれば】線形識別不可能な問題も解くことができる」ことを示すために挙げました。
ただ、多層パーセプトロンの学習において、通常は単純パーセプトロンと同じ手順で重みを求めることはできません。
XOR問題は非常に単純な問題なので「中間層のユニットがどのような値を出力してほしいか？」や「各重みがどういった値になってほしいか？」が明らかでしたが、一般にそういったことはほぼあり得ないからです。（教師データが与えるのは「入力層に入力するパラメータ」と「出力層から出力される値に対応する正解ラベル」のみです。中間層ユニットの各出力に対応する正解ラベルはありません。）
というわけで、実際に重みを求める方法は次回解説します。

多クラス分類

ここまでの単純パーセプトロンの例では、SPAM識別や論理演算を扱いました。
これらはパラメータ（グラフの各点）を2つに分類する行為（SPAM/非SPAM、真/偽など）なので、2クラス分類や二値分類などと呼びます。
これに対し、3つ以上に分類することを多クラス分類と呼んで区別したりします。

前回学んだ単純パーセプトロンで多クラス分類を行うには、分類すべきクラス数と同じ数だけ単純パーセプトロンを準備し、各入力に対してそのうち1つだけが発火（1を出力）するよう学習すればよいです。
入力に対し、単純パーセプトロンAは「クラスAに属するか否か」を判定、単純パーセプトロンBは「クラスBに属するか否か」を判定…という具合です。
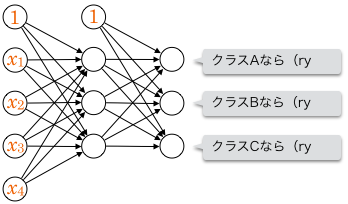
4次元の入力をもとに3クラスに分類する例を図示するとこうなります。

単純パーセプトロンで多クラス分類

ユニットの出力が別のユニットの入力になっていないという意味で、上記は多層パーセプトロンとは言えないことに注意してください（そのことがわかりやすいよう、上図では単純パーセプトロンの1つに色づけをしてあります）。
単純パーセプトロンが複数あるだけなので、各クラスに属するか否かがそれぞれ線形識別可能な問題でなければ学習できません。
一方、多層パーセプトロンで多クラス分類を行えば、線形識別不可能であっても分類できることがあります。

多層パーセプトロンで多クラス分類

正解ラベルは、ベクトルを使って $\bm{t} = \left( \begin{array}{c} 1 \\ 0 \\ 0 \end{array} \right)$ のように表現することができます。
この場合は出力層の1つめのユニットだけが1を出力すれば正解という意味です。

このようにして、例えばメール中の各単語の数をもとに自動でメールをカテゴリ分類する仕組みなどが作れます。
カテゴリ分けではなくタグ付けにするのであれば、出力層の複数ユニットが同時に1を出力することを許容してもいいですね。
多層パーセプトロンによってどのような問題が解けるかを考えると楽しいと思います。

次回は、実際に多層パーセプトロンでどのように重みを更新していくのか、その手順を書きます。

「例えば」と書いたのは、実際にはグラフ上の点を分割する直線の式は無数に存在するからです。傾きや位置が多少ずれても分割できたりしますし、同じ直線になるような重みも無限に考えられます。 ↩
なぜ線形分離不可能な問題が解けるかというと、「結果的に中間層で線形分離可能な形に変換されているから」と言うこともできます。 ↩
より広い意味の言葉として「ニューラルネットワーク」がありますが、多層パーセプトロンはその中でも
・情報の伝達が一方向にのみ行われる
・ユニットが層状に配置される
・再帰的な接続を持たない
といった特徴を持ちます。 ↩