高卒でもわかる機械学習 (2) 単純パーセプトロン

単純パーセプトロン

動物の神経細胞（ニューロン）は、樹状突起という部位で他の細胞から複数の入力を受け取り、入力が一定値以上に達すると信号を出力する（これを「発火する」と言ったりします）とされており、それをモデル化したものとして形式ニューロンというものが提案され、さらに応用してパーセプトロンというモデルが発明されました。¹
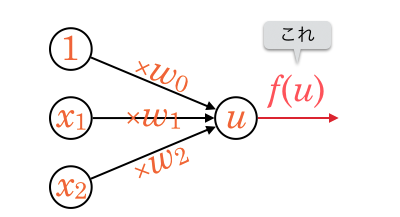
と、難しそうなことを書きましたが、ざっくり絵にするとこんな感じです。

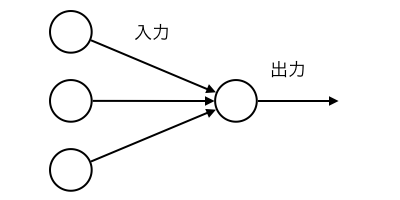
パーセプトロン

絵では入力が3つになっていますが、実際にはいくつでも構いません。
前回の $w_0 + w_1 x_1 + w_2 x_2 + \cdots$ の問題は、このモデルにあてはめることができます。

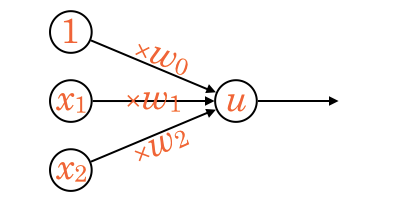
パーセプトロン

入力ノードが $1, x_1, x_2, \cdots$ 、入力途中の矢印が $w_0, w_1, w_2, \cdots$ に対応しています。
$1, x_1, x_2, \cdots$ を入力として受け取り、それぞれに $w_0, w_1, w_2, \cdots$ を掛けた後、中心のノードですべて足し合わせます。
この値を $u$ とします。

$u = w_0 + w_1 x_1 + w_2 x_2 + \cdots$

前回のSPAMの例だと、正しく学習された後であれば、SPAMの場合 $u > 0$ 、非SPAMの場合 $u < 0$ となるはずですね。
このようなモデルで表現できる学習機械を単純パーセプトロンと呼びます。
これがいわゆるニューラルネットワークの基本単位となります。

重みベクトルの更新

こうして見ると、SPAMフィルタにおいて学習後の $w_1, \cdots , w_n$ は相対的に各単語の「SPAMっぽさ」を表す値になっていることがわかるでしょうか。
$x_1, \cdots , x_n$ はメール中の注目した各単語の数でした。
例えば $x_1$ と $x_2$ が同じ値（単語数）だったとしても、 $w_1$ より $w_2$ の絶対値の方が大きければ、 $x_2$ が $u$ に与える影響は大きくなります。つまり、一般的に $w_1, \cdots , w_n$ は各入力値 $x_1, \cdots , x_n$ の重みを表していると言えます。²
$w_0$ は入力と結びついていないバイアスと呼ばれる値なのですが、ここではこれもまとめて重みと考えてしまいましょう。
というわけで、ベクトル $\bm{w} = \left( \begin{array}{c} w_0 \\ w_1 \\ \vdots \\ w_n \end{array} \right)$ を、重みベクトルと呼びます。

$1, x_1, x_2, ..., x_n$ をパーセプトロンに入力したときに出力される値を教師データと見比べながら、 $w_0, w_1, w_2, ... , w_n$ を更新していきます。
では、実際にはどのように $\bm{w}$ を更新していけばいいのでしょうか？
簡単に言うと、

$w_0, w_1, ... , w_n$ にそれぞれランダムな値を設定する
下記を繰り返す
- 教師データを読み込ませ、出力が正しくなければ、重みの値を「正しそうな方向」に少しずらす
- 全教師データについて正しい出力が行われたら繰り返し終了

という手順なのですが、単純パーセプトロンの場合、繰り返しの中で重みを「正しそうな方向」に更新する式は非常に簡単です。
ただしここでは、その式を記載する前に、次回以降に学ぶ多層パーセプトロンでも活用できるよう、更新式を導き出す一般的な考え方についてまずは説明します。

勾配降下法

まず、「ある教師データを読み込ませたときの出力がどれくらい期待外れだったか？」を数値で返す関数 $E$ があるとします。
これを誤差関数、あるいは損失関数と言ったりします。

$E = ???$

$\bm{w}$ などを含む式で表現され、0以上の値を返すようにするのが普通です。
この関数は「出力が期待外れであるほど大きな値を返す」ものであれば何でも良いといえば良いのですが、定義次第で後の計算での扱いやすさが変わってきます。
実際の定義は次項で行いますね。

誤差関数の出力値は「期待外れの度合い」ですから、それを最小にできれば学習完了したと見なせます。
$\bm{w}$ をランダムな値で初期化してから少しずつ動かしていき、誤差関数の出力値を最小にすることを考えます。

$\bm{w}$ の要素の1つ $w_i$ に注目し、 $w_i$ と誤差関数の出力値の関係をグラフにすると下記のようになったとします。（ $w_i$ 以外の変数は固定されていると考えます。）

勾配降下

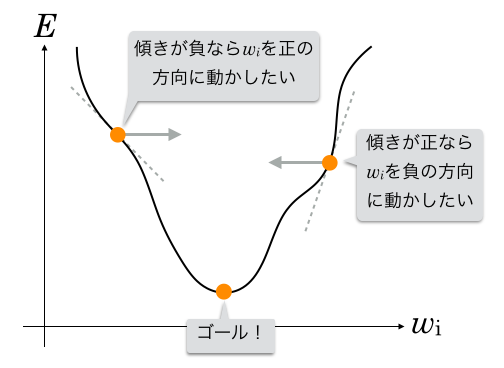
このグラフで「誤差 $E$ が一番小さくなる $w_i$ 」は曲線が下方向に突起している箇所なので、目指したいのはここです。³
グラフ中にも記載がありますが、

現在の $w_i$ でグラフの傾きが正の場合 → $w_i$ を負の方向に動かす
現在の $w_i$ でグラフの傾きが負の場合 → $w_i$ を正の方向に動かす

とすれば、誤差が一番小さくなる $w_i$ に辿り着くことができそうです。
傾きとは、微分値 $\frac{\partial E}{\partial w_i}$ です。
そこで、下記の更新式を考えてみます。⁴

更新式（仮）: $w_i \gets w_i - \frac{\partial E}{\partial w_i}$

微分値、つまり傾きが正の時は $w_i$ が負の方向に動き、負の時は $w_i$ が正の方向に動くようになりました。
また、傾きの絶対値が大きいときは大きく変化し、小さいときは小さく変化します。
ただ、これだと更新量が大きすぎてうまく収束しないので、小さな正の定数 $\rho$ を決めて、微分値に掛けることで更新量を調整します。

更新式（決定版）: $w_i \gets w_i - \rho \frac{\partial E}{\partial w_i}$

$w_0 \dots w_n$ をベクトル $\bm{w}$ としてまとめて書いてしまうとこうです。

更新式（決定版・改）: $\bm{w} \gets \bm{w} - \rho \frac{dE}{dw}$

この $\rho$ を学習率といいます。
1より小さな値を設定するのが普通ですが、あまりにも小さいと更新量も小さくなり計算の回数が増えてしまうのでご注意ください。⁵

こうして誤差が最小になったと思われるまで繰り返し $w_i$ を変化させていくのです。
この方式を勾配降下法といいます。⁶
この更新式からわかるように、 $E$ の定義は $\bm{w}$ で微分したときに計算が簡単な式になる形が望ましいです。

あとは、誤差関数が決まれば実際の更新式も決まりますね。

単純パーセプトロンにおける誤差関数

単純パーセプトロンにおいて、1組のパラメータに対する誤差関数は下記で定義できます。

$E = \max (0, -t\bm{wx})$

$\max (a, b)$ は、 $a$ と $b$ のうち大きい方を出力する関数です。
$t$ は教師データの正解ラベルで、次のように定義します。

$t = \begin{cases} 1 & (\mbox{SPAM}) \\ -1 & (\mbox{not SPAM}) \end{cases}$

真偽値っぽく 0, 1 にしたい人もいるかも知れませんが、 -1, 1 なのが重要です。

なぜ $\max (0, -t\bm{wx})$ が誤差関数として使えるのでしょうか？

$x_1, x_2$ の2次元で考えてみます。
まず、繰り返しになりますが、 $\bm{w x}$ （つまり $w_0 + w_1x_1 + w_2x_2$ ）の値は、 $\bm{w x} = 0$ の直線上では当然 0、直線で分割された片方のエリアでは正の値、もう一方では負の値になります。そして、ラベルが1の点はすべて正のエリアに、ラベルが-1の点はすべて負のエリアに入ると学習完了です。

下図をご覧ください。

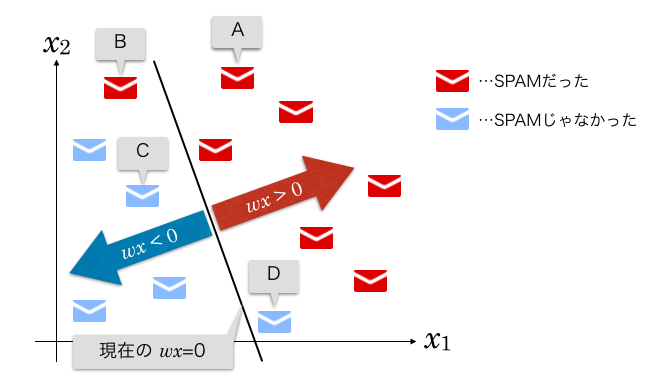
重み更新途中のグラフ

これは学習が完了していない状態のグラフで、BとDの点が誤分類されている様子を表しています。
まずAの点に注目してみます。
このメールは SPAM ですが、現在の識別関数で正しく分類されており、 $\bm{w x} > 0$ です。
正解ラベル $t$ は 1 ですから、
$-t\bm{wx} = -\bm{wx} < 0$ です。よって
$E = \max (0, -t\bm{wx}) = 0$ となり、誤差が0という結果になります。

同じように、A〜D各点について表にまとめてみます。
（「正解？」というのは、「現状で正しく分類されているか？」という意味で書いてます。）

	SPAM？	$t$	正解？	現状の $\bm{wx}$	$-t\bm{wx}$	$E = \max (0, -t\bm{wx})$
A	$\mbox{Yes}$	$1$	$\mbox{Yes}$	$\bm{wx} > 0$	$-t\bm{wx} = -\bm{wx} < 0$	$E = 0$
B	$\mbox{Yes}$	$1$	$\mbox{No}$	$\bm{wx} < 0$	$-t\bm{wx} = -\bm{wx} > 0$	$E = -\bm{wx} = \|\bm{wx}\|$
C	$\mbox{No}$	$-1$	$\mbox{Yes}$	$\bm{wx} < 0$	$-t\bm{wx} = \bm{wx} < 0$	$E = 0$
D	$\mbox{No}$	$-1$	$\mbox{No}$	$\bm{wx} > 0$	$-t\bm{wx} = \bm{wx} > 0$	$E = \bm{wx} = \|\bm{wx}\|$

この誤差関数は、ある点 $x$ が正しく分類されていれば 0 を返し、正しく分類されていなければ $|\bm{wx}|$ を返すことがわかると思います。⁷

では、この $|\bm{wx}|$ というのは何を表しているのでしょうか？
実は、この値はグラフ上の点から直線への距離に比例しているのです。⁸⁹
感覚的にも、 $\bm{wx} = 0$ の直線に近い点ほど $\bm{wx}$ の値も 0 に近いというのは腑に落ちやすいのではないでしょうか。
この誤差関数は、ある点が期待と逆側に分類されてしまっているときに、直線からの距離が大きければ誤差も大きいと見なし、距離が小さければ誤差も小さいと見なすということを意味します。

単純パーセプトロンの学習アルゴリズム

誤差関数 $E$ が定まったので、重みの更新式を作れるようになりました。
一般に、重みの更新式は下記でした。

$\bm{w} \gets \bm{w} - \rho \frac{dE}{d \bm{w}}$

$E = \max (0, -t \bm{w} \bm{x})$ は、誤差がない場合は 0 を、誤差がある場合は $-t\bm{wx}$ を返します。
誤差がない場合を無視し、 $\bm{w}$ の1要素 $w_i$ に注目すると、

$\begin{align*} \frac{\partial E}{\partial w_i} & = \frac{\partial (-t\bm{wx})}{\partial w_i} \\ & = \frac{\partial (-t w_0 - t w_1 x_1 - t w_2 x_2 - \dots - t w_i x_i - \dots - t w_n x_n)}{\partial w_i} \\ & = -t x_i \end{align*}$

なので、更新式は下記です。

$w_i \gets w_i + \rho tx_i$

ベクトルでまとめて表現するとこうです。

$\bm{w} \gets \bm{w} + \rho t \bm{x}$

以上を踏まえると、単純パーセプトロンの学習アルゴリズムは下記のようになります。

$w_0, \dots ,w_n$ をランダムで設定
each 全教師データ
- 教師データのを入力し、出力が正解と合っているかチェック
  - 合っていた場合、何もしない
  - 合っていなかった場合、 $\bm{w} \gets \bm{w} + \rho t\bm{x}$
上記のループ内での更新があったか？
- あった場合、もう一度上記のループを最初から
- なかった（すべて正解だった）場合、終了

活性化関数

単純パーセプトロンにおいてはあまり意識しなくても実装できるのですが、パーセプトロンのユニットは、 $u$ の値に応じて何らかの値を出力します。

パーセプトロンの出力

この出力値を決定する関数を活性化関数といいます。
問題に応じて適切な関数を使用します。
最もシンプルな活性化関数は、 $u$ をそのまま出力する関数です。

$f(u) = u$

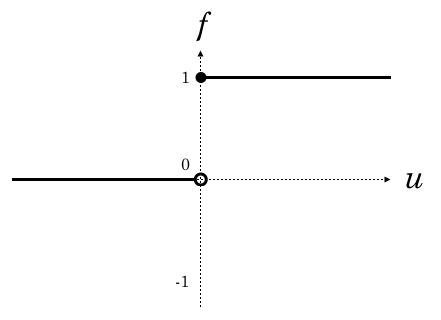
今回のSPAM識別のような二値分類では、単位ステップ関数という下記がシンプルです。

$f(u) = \begin{cases} 1 & (u \geq 0) \\ 0 & (u < 0) \end{cases}$

グラフにするとこんな感じです。

ステップ関数グラフ

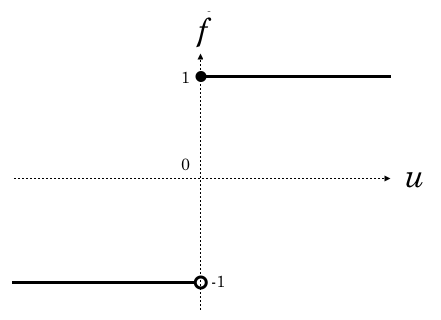
ただ、正解ラベルは1と-1だったので、それに合わせてこういう関数にした方がわかりやすい実装になるかも知れません。¹⁰

$f(u) = \begin{cases} 1 & (u \geq 0) \\ -1 & (u < 0) \end{cases}$

グラフにするとこうなりますね。

ステップ関数2

これら2つのグラフの形は、「入力がある値を超えたら急激に発火する」という動物の神経細胞の動きに似ています。
次回以降で学ぶ多層パーセプトロンでは、この活性化関数をどのように選ぶかが重要になってきます。

両者の違いを簡単に述べると、形式ニューロンは入出力が0または1のみであるというのと、バイアス（この記事で $w_0$ としているもの）の扱いが少し違います。また、「パーセプトロン」に関しては、1958年に発表されたそうですが、その後様々な応用が提案される中で厳密な定義は曖昧になってきている印象です。あまりこだわらないのがよさそうです。 ↩
例えばSPAM識別において「出会い」という単語の重みはとても大きくなるでしょう。
SPAMか否かに影響を与えない単語の重みは0に近くなるはずです（その単語はパラメータとして無意味ということでもあります）。
また、「この単語があればSPAMの可能性はむしろ減る…」というような単語がもし存在するなら、その重みは負の値になるかも知れません。 ↩
厳密には勾配降下法で辿り着けるのは極小値なので、必ずしもそれが最小値になるとは限りません。ただし、単純パーセプトロンで線形分離可能な問題を解く場合はそこの心配は要りません。より複雑な問題では、極小値が複数ある場合を考慮する必要が出てきたりもします。 ↩
左向きの矢印は代入を表します。 ↩
実際の問題ではうまく収束させるために学習率を動的に変化させたりします。
また、ここで挙げた更新式が基本ではありますが、より確実に最小値を目指すためや、計算量を減らすためなどの、様々な改善テクニックがあります。 ↩
勾配降下法を適用するアルゴリズムによって、さらに下記のように呼び分けられます。
最急降下法
一般に勾配降下法によって関数の極小値を目指す手法を言いますが、機械学習においては、まず全教師データを読み込ませ、各々の誤差の合計値（または平均値）を算出してから、それを最小化していく手法を指すようです。
このような学習法を一括（バッチ）学習と呼びます。
確率的勾配降下法
一部の教師データのみ（典型的には1件のみ）を読み込ませ、その誤差をもとに1回だけ更新を行い、次の教師データを読み込ませ…ということを繰り返す手法です。
逐次（オンライン）学習またはミニバッチ学習に分類される学習法です。 ↩
$|a|$ は $a$ の絶対値を表します。 ↩
$\bm{w}$ を定数、 $\bm{x}$ を変数として考えた場合です。 $\bm{w}$ の変化も考慮に入れると、比例するとは言えなくなります。 ↩
点 $(x_{a1}, x_{a2})$ から直線 $w_0 + w_1 x_1 + w_2 x_2 = 0$ への距離は
$\frac{|w_0 + w_1 x_{a1} + w_2 x_{a2}|}{\sqrt {{w_1}^2 + {w_2}^2}}$ で表せます。
この公式の証明は検索するといろいろ出てきます。 ↩
$\geq$ は ≧ と同じです。 ↩