高卒でもわかる機械学習 (4) 誤差逆伝播法の前置き

前回からだいぶ時間が空いてしまいました。
誰も見てないものかと…

多層パーセプトロンの学習法として使われる誤差逆伝播法について書いていきますが、この記事シリーズのルール「長いけど平易」を守るとけっこうな長さになったので、分割して掲載します。
今回は一言で言えば誤差逆伝播法の理論で使う記号の定義をするだけです。
しかし僕のような数式に慣れていない人間にとっては、実はここが一番の難関かも知れないとすら思っているので、腰をすえてじっくりやろうと思います。
正念場です。

活性化関数

先にこの項のまとめを書いておくとこうです。

多層パーセプトロンの活性化関数は微分できることが重要
有効な活性化関数にはいろいろある
ひとまずこの記事では活性化関数を $f$ 、その導関数を $f'$ と一般化して記述する

それだけなのですが、せっかくなのでそのあたりの現状に軽く触れておこうと思います。

活性化関数とは、ユニットの出力値を決める関数のことでした。

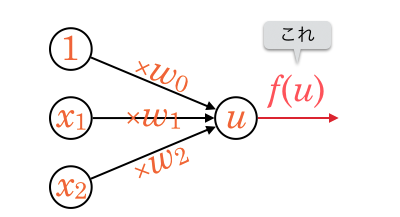
perceptron_activate

$u = w_0 + w_1 x_1 + w_2 x_2 + ... + w_n x_n$

$f(u) = ???$

単純パーセプトロンの説明では、次のようなステップ関数を活性化関数として挙げました。

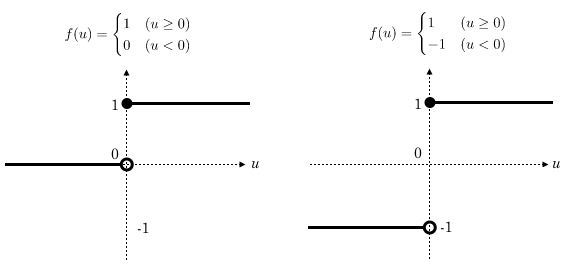
ステップ関数

単純パーセプトロンの説明で、1つのユニットは $u$ （ = $\bm{w} \bm{x}$ ）が 0 より大きいか小さいかで入力を評価するものとしました。これらのステップ関数の定義はそれにマッチしています。
そしてこれらは動物の神経細胞の発火状態と非発火状態を大幅に簡略化して表現したものとみなすことができます。

しかし実は、多層パーセプトロンではこの活性化関数が使えません。
詳細は次回解説しますが、学習時に活性化関数の“微分値”が重要になるからです。
ステップ関数だと有効な微分値が導けません。¹
そこで、多層パーセプトロンでは下記のような活性化関数がよく使われてきました。
左はシグモイド関数、右は双曲線正接関数と呼ばれるものです。

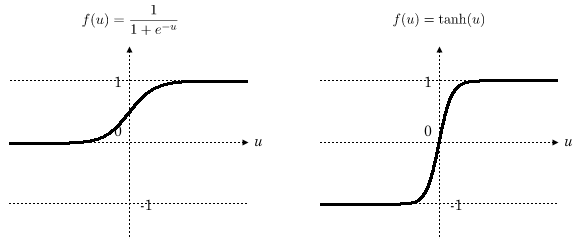
シグモイドと双曲線正接

式自体にはあまり意味がないと思っていいです。グラフの形に注目してみましょう。²
どちらも
・0を境に急激に変化している
・出力値の範囲
という点は前述のステップ関数と似ていますが、グラフが滑らかな曲線になっています。
グラフが滑らかなのは微分可能な関数の特徴ですね。
また、出力が0と1の二値ではなく連続値³をとることに注意してください。

さらに近年、中間層においては下記のような活性化関数を用いるとよいことが発見されました。
ReLU（Rectified Linear Unit）と呼ばれるものです。⁴

relu

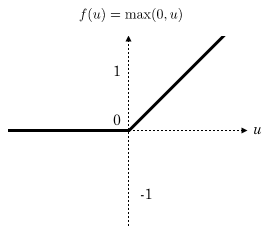
上記は数学的に言うと微分可能ではありませんが、プログラム上では下記のように微分値を定義することができます。

$\frac{df}{du} = \begin{cases} 1 & (u \geq 0) \\ 0 & (u < 0) \end{cases}$

また、層内の出力値を全て足し合わせると1になるよう調整するソフトマックス関数や、層内の複数の出力値の中で最も大きい値を出力するMaxoutなど、同じ層にある他のユニットの影響も受けるような活性化関数もあります。

各々の解説は別記事に譲りますが、活性化関数についてはこのように様々な提案がされている状況ですので、今回の記事では活性化関数の具体的な定義をせず、 $f(u)$ という形で統一して記述することにします。⁵
また、 $f$ の導関数を $f'$ とします。

各記号の再定義

各ユニットの重みと出力値

多層パーセプトロンでは、大量のユニットと、それら各々に紐づく重みの値を扱う必要があります。
これまで使ってきた $w_0, w_1, w_2, \dots$ などの、添え字が1つだけの記号では足りないので、ここで新たに記号を割り当てなおします。
新しい記号では添え字をたくさん使うので、これが式の中に現れると何だかとてつもなく難しく見えてしまいます。
ただし、添え字のせいで難しく見えるだけで、式自体はこれまでの知識で理解できるものなので、図を見ながら把握してみてください。

まず、入力層を除く層の数を $L$ とおき、入力層を第0層、その次を第1層…というように呼ぶことにします。出力層が第 $L$ 層ということになります。
そして、任意の第 $l$ 層のユニット数（固定で1を出力しているものを除く）を $N^{(l)}$ のように表記します。
第3層ならユニット $N^{(3)}$ 個です。
右上に数字がありますが累乗ではなくただの添え字です。累乗と区別するためにカッコをつけています。

次に、第 $l$ 層の $i$ 番目のユニットに注目します。（下図参照）
このユニットの出力値を $o_i^{(l)}$ とします。
そしてこのユニットに紐付いている重みのうち、 $j$ 番目のものを $w_{i, j}^{(l)}$ と表現します。⁶
文字がたくさん組み合わさっていますが、1つの記号と見なしてください。添え字が3つあるだけです。
右下の2つの添え字の範囲は、1番目が 1〜 $N^{(l)}$ 、2番目が0〜 $N^{(l-1)}$ となります。

このユニットへの入力は、1つ前の層の出力値なので、 $1, o_1^{(l-1)}, o_2^{(l-1)}, \dots$ のようになります。
これらの入力値に重みをかけて合計した値を $u_i^{(l)}$ とします。

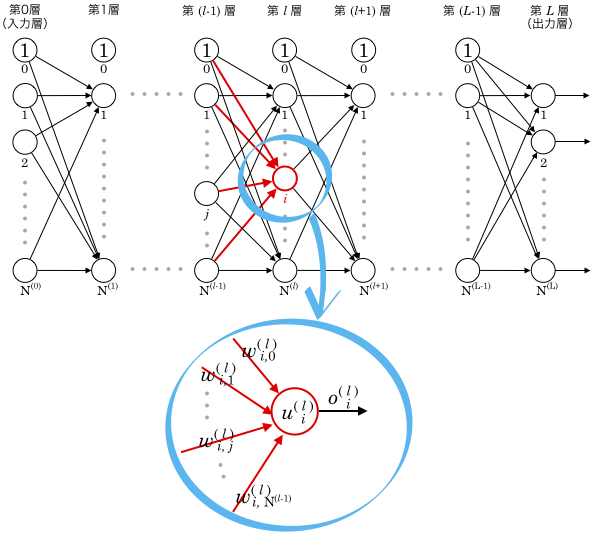
mlp_name

添え字が多くて把握するのが大変ですが、せめて

右上の添え字は層番号
右下の添え字の1番目は層内でのユニット番号

というのは統一してみました。

関係を式で表してみる

1つのユニットは単純パーセプトロンと同じ動作をしますから、以上の記号の関係を式で表すと下記のようになります。

$o_i^{(l)} = f(u_i^{(l)})$

$u_i^{(l)} = w_{i, 0}^{(l)} + w_{i, 1}^{(l)} o_1^{(l-1)} + w_{i, 2}^{(l)} o_2^{(l-1)} + \dots + w_{i, N^{(l-1)}}^{(l)} o_{N^{(l-1)}}^{(l-1)}$

添え字が多すぎて書いてる方もイヤになってきました。最後の項なんかは添え字にも添え字がついています！
ただ、繰り返しますが、式自体の難しさはこれまでと変わりません。

上記の2行目の式を、今回だけ (A) 式と名付けます。
この式の中に $(l-1)$ 層目の各ユニットの出力値が現れていますね。
$(l-1)$ 層目の $j$ 番目のユニットに注目すると、その出力値は、さらに $(l-2)$ 層目の出力値を使って下記のように表現できます。

$o_j^{(l-1)} = f(u_j^{(l-1)})$

$u_j^{(l-1)} = w_{j, 0}^{(l-1)} + w_{j, 1}^{(l-1)} o_1^{(l-2)} + w_{j, 2}^{(l-1)} o_2^{(l-2)} + \dots + w_{j, N^{(l-2)}}^{(l-1)} o_{N^{(l-2)}}^{(l-2)}$

これを (A) 式の $o_1^{(l-1)}, o_2^{(l-1)}, \dots$ に代入していくとかなり長い式になります。
そして $(l-2)$ 層目の各出力値は、さらに $(l-3)$ 層目の出力値を使った式で表現できます。
そうやって展開していくと、最終的に入力層のパラメータを使った式が導けることがわかるでしょうか。
しかしとてつもなく長い式になりそうですね。
実際に式を導く必要はありませんが、そのように式展開できるということだけ理解しておいてください。

和の記号を使う

和の記号 $\displaystyle \sum$ を使うと、(A)式はよりシンプルに書くことができます。

$u_i^{(l)}=\sum_{k=0}^{N^{(l-1)}} w_{i, k}^{(l)} o_k^{(l-1)}$

$k$ が添え字として使われている位置を見ると、その値の範囲は書かなくても明らかなので、省略して書いたりもします。

$u_i^{(l)}=\sum_{k} w_{i, k}^{(l)} o_k^{(l-1)}$

ネットワークの入力と出力

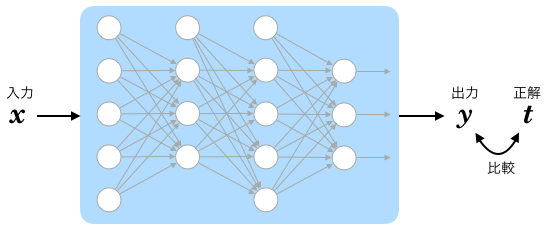
多層パーセプトロンは、ネットワーク全体で1つの学習機械です。
このネットワーク（の入力層）にパラメータを入力し、（出力層から）出力されるのがより適切な値になる状態を目指すことになります。

ネットワークへの入力パラメータをベクトル $\bm{x}$ とします。
このベクトルの要素はそのまま入力層の各ユニットの出力値となりますから、下記のように表現できます。

$\bm{x} = \left( \begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_{N^{(0)}} \end{array} \right) = \left( \begin{array}{c} o_1^{(0)} \\ o_2^{(0)} \\ \vdots \\ o_{N^{(0)}}^{(0)} \end{array} \right)$

ネットワークの出力値をベクトル $\bm{y}$ とします。
このベクトルの要素は出力層の各ユニットの出力値ですから、同じく下記のようになります。

$\bm{y} = \left( \begin{array}{c} y_1 \\ y_2 \\ \vdots \\ y_{N^{(L)}} \end{array} \right) = \left( \begin{array}{c} o_1^{(L)} \\ o_2^{(L)} \\ \vdots \\ o_{N^{(L)}}^{(L)} \end{array} \right)$

出力層の出力値に対する正解ラベルは $\bm{t} = \left( \begin{array}{c} t_1 \\ t_2 \\ \vdots \\ t_{N^{(L)}} \end{array} \right)$ とします。
$t_1, t_2, \dots , t_{N^{(L)}}$ は、単純パーセプトロンの時のような 1 と -1 の二値ではなく、より一般的に「出力されてほしい理想の値」がそれぞれ入っていると考えます。
なお、中間層の出力値に対する正解ラベルは存在しないことに注意してください。

ネットワークの入力と出力

次回はいよいよ実際の学習法の理論に入ります。

$u = 0$ の点で微分不可能というだけでなく、それ以外の点でも微分値が0になってしまいます。 ↩
グラフの特徴がよく見えるように、縦横の比率を意図的に操作しています。 ↩
コンピューター上では浮動小数などで近似されます。 ↩
シグモイド曲線を見ると、パラメータの絶対値がある程度大きくなると微分値が0に近くなってしまうのがわかります。このために重みの更新がなかなか進まないのが欠点なのですが、次回解説する誤差逆伝播法が理解できたら、なぜなかなか進まないのかを考えてみてください。ReLUが解決した問題はそこです。また、ReLUは微分値の計算コストも低いです。 ↩
出力層と中間層で異なる活性化関数を用いるのが普通ですが、簡単のため、この記事ではそれをいったん無視します。 ↩
当然と言えば当然ですが、記号の定義が資料によって違うのと同じく、添え字の位置関係も記述者によってまちまちですので注意してください。例えば $w$ の右下にはカンマ区切りで添え字が2つありますが、これの位置が逆転している資料も多いです。 ↩