はじめに
多層パーセプトロンの重みを更新する理論について解説します。
更新すべき重みがたくさんあるので単純パーセプトロンより難しいですが、ここがわかると近年流行したディープラーニングを理解するための基本ができあがります。
ただし、結構長いので、「理論はざっくりでいいから最終的に使える重み更新式が知りたい」という人は、別のサイトや本を読むのをお勧めします。
なお、記事中で使われる各種記号の定義は前回やりましたので、わからなくなったらそちらを参照してください。
数学の前知識
今回は数式がけっこう出てきます。
そこで必要な数学知識について、いくつか説明を書いておきます。
簡単のため前提条件を少し省略しているので、数学的に厳密ではない箇所はご容赦ください。
偏微分
偏微分は以前の記事でも出てきましたが、僕が誤解してまして、高校数学の範囲には含まれていないようでした。
そんなに難しいことではなく、複数の変数による関数があるとして、その中の1つの変数のみに関する微分のことです。
例えば として、
の
に関する偏微分は
です。
以外の変数はすべて定数と見なすので、
を含まない項は消えています。
微分の記号は の代わりに
を使います。
合成関数の微分公式
こちらは高校数学の範囲内だと思いますが、復習しておきます。
が
の関数で、さらに
が
の関数とします。
このとき、 を
で微分した
について、下記のような公式があります。
合成関数の偏微分公式
これは大学数学の範囲だと思います。
が
の関数(複数変数を持つ)で、
がそれぞれ
の関数である場合、
を
で偏微分すると下記のようになります。
これをこの記事では合成関数の偏微分公式の「難しい方」と呼ぶことにします。
(他所で言うと笑われるのでご注意ください。)
さらにこれの特殊ケースとして、「簡単な方」があります。
のうち、実は
番目のみが
の関数で、ほかは
の影響を受けない場合を考えます。
を表す式が
を含まないのであれば、
を
で偏微分すると 0 になりますね。
つまり、 の中の
は、
の場合はすべて 0 になるので、
の場合だけを考慮すればよくなります。
高校で習う方の公式とほぼ同じ形をしています。
繰り返しますが、偏微分において上記は特殊なケースです。
が、今回は何度か出てきます。
使い方のポイントは下記です。
- 関数
の変数
〜
のうち、
が影響するのが1つだけだったら「簡単な方」を使う
- 関数
の変数
〜
のうち、
が影響するのが複数だったら「難しい方」を使う
- 難しい方には
がつく
勾配降下法の式
ここから本題です。
単純パーセプトロンの説明で、勾配降下法について説明しました。
多層パーセプトロンにおいても、その理論を用いて重みを更新します。
前回新たに定義した記号を用いて勾配降下法の式を書き直すと、下記のようになります。
は任意の層番号、
は層内でのユニット番号、
はユニット内での重みの番号(= 1つ前の層のユニット番号)です。
は誤差関数ですが、単純パーセプトロンと同じ誤差関数が使えないため、新しく定義します。
多層パーセプトロンの誤差関数
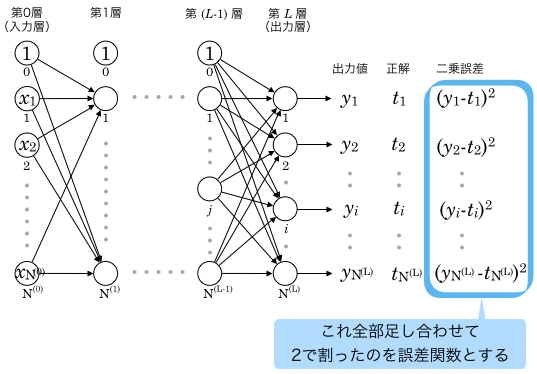
多層パーセプトロンはネットワーク全体で1つの学習機械ですから、誤差関数も全体で1つだけ定義します。
誤差関数は次のように定義されます。1
は出力層
番目のユニットの出力値ですから、
はそのユニットの「理想の出力値と実際の出力値の差」です。
まずそれを二乗しています。二乗しているのは後の計算で都合がいいからです。負の値にならないメリットもありますね。
は、出力層の全ユニットについてその計算をして足し合わせるということです。2
そしてさらに をかけています3。これも後の計算で都合がいいからという理由です。
誤差を二乗した値の和(の定数倍)なので、このを二乗誤差と呼びます。
番目のユニットのみに注目した場合の
も二乗誤差と言ったりしますが、あまり気にしないでください。
ですから、次のようにも書けます。
これは、 が
の関数であることを意味しています。
出力層の重み更新
誤差関数が決まったので、勾配降下法を適用することを考えます。
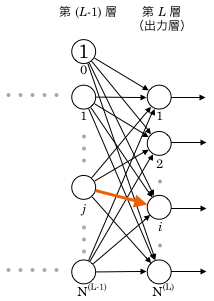
まず、出力層番目のユニットの
番目の重み、
に注目します。
更新式の展開
この重みの勾配降下法による更新式は
です。
この中の を解いていきます。
は
の関数、
は
の関数、
は
の関数と見なせます。
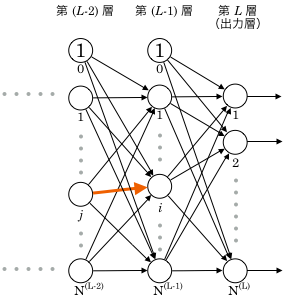
また、は出力層
番目以外のユニット出力値も変数として持ちますが、上図を見ると分かるとおり、
の影響は
番目のユニット以外には及びません。
よって、合成関数の偏微分公式の「簡単な方」を使い、下記が成り立ちます。
3項に分解できました。1項ずつ見てみましょう。
後ろの項の方が今までの知識で理解できるので、後ろから順にいきます。
第3項: 
は、出力層の一つ前、つまり第
層の各ユニット出力に重みをかけて合計したものなので、下記のようになります。
第2項: 
は出力層
番目のユニットの出力ですから、
です。
つまりこれは活性化関数の微分です。4
実際の式は活性化関数の定義によって決まります。
第1項: 
出力層 番目のユニット出力値
(
)で誤差関数
を偏微分するということです。
下図をご覧ください。
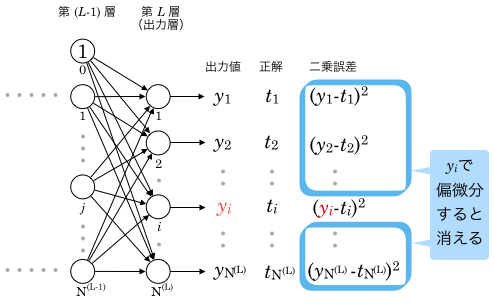
誤差関数は、出力層すべてのユニットの二乗誤差を合計して
したものでした。
これを(
)で偏微分すると
以外の変数はすべて定数と見なして消えるので、
番目以外のユニットの二乗誤差はすべて無視することができます。
よって、
となります。5
2行目で番目以外の項を消しています。
出力層ユニットの重み更新式
以上より、
なので、これを勾配降下法の式に当てはめると、 の更新式は下記になります。
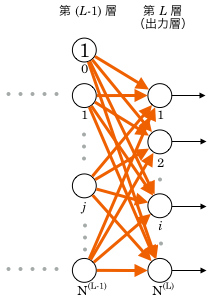
複雑に見えますが、プログラムとして実装すると大したことはありません。
,
の値を変えていくと、出力層ユニットにひもづく重みはすべて更新できます。
出力層より1つ前の層の重み更新
上記の式で多層パーセプトロン内のすべての重みが更新できるといいのですが、出力層以外の重みには別の更新式が必要になります。
出力層より一つ前の層、つまり第層のユニットに紐付く重みについて考えます。
ここでも前出の誤差関数 を使って勾配降下法を適用します。
第層向けに誤差関数を新しく定義したりはしません。
第層
番目のユニットの
番目の重み、
に注目します。
なお、前の節でも ,
という記号を使いましたが、今回の
,
はそれとは別だと思ってください。
新たに記号を定義するのが大変なので使い回しています。
更新式の展開
この重みの勾配降下法による更新式は
です。
前回少し触れましたが、出力層の出力値は、第層の出力値を使った式に展開することができます。
つまり誤差関数中に現れる もすべて
を含む式に展開できるということです。
その状態ので考えてみます。
展開後の式はとても長くなるのでどんな式かはハッキリわからなくていいですが、 が消えて
の関数になっていることだけ意識しておいてください。
は
の関数であり、また、
は
の関数で、
は
の関数です。
そしてこの は第
層
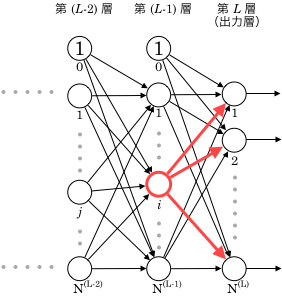
番目以外の出力値も変数として持ちますが、 上の図を見るとわかるように、
が影響を与えるのは、第
層だと
番目のユニットだけです。(第
層まで伝播すると複数のユニットに影響しますが、
は今
から消えているのでした。下記では、微分のパラメータとしても 第
層に関する変数を使っていません。)
よって、合成関数の偏微分公式の「簡単な方」を使って下記のように展開できます。
これも後ろから一項ずつ見ていきます。
第3項: 
これは層番号が違うだけで、出力層の時と同じパターンです。
第2項: 
これも同じですね。層番号だけが違います。
第1項: 
これが出力層より少し厄介です。
第層
番目のユニット出力値で誤差関数を偏微分しています。
を
の関数と見なしているのでしたが、この関数はよくわからないくらい長いのでした。
このままだと計算がしにくいので、改めて を元の定義(
の関数)に戻し、合成関数の偏微分公式でさらに分解します。
使うのは難しい方です。
「難しい方」を使ったのは、 が第
層のユニットすべてに影響を与えるからです。
もう少し解いてみる
上記の式、中の第三項、
を解きます。
は第
層の各ユニット出力に第
層
番目のユニットの重みを掛けて合計したものなので、
です。
これを前述の式に代入すると下記のようになります。
の中に、偏微分の記号を使った項があと2つ残っていますね。
この2項の中の各変数を見てみると、すべて層番号が となっています。
実はこの2項、第層の重み更新を計算する際にすでに算出していることにお気づきでしょうか?
それがポイントになってきます。
誤差逆伝播法の発想
流れでいくと第層の重み更新式を記載したいところですが、ここであえて多層パーセプトロンの学習法の概要を書きます。
第層の重み更新を先に計算すると、その計算結果の一部を第
層の重み更新の際に利用できそうでした。
プログラム上では一時変数に保持しておけば使えますね。
それを使って第層の重み更新の計算をし、さらにその計算結果の一部を第
層の重み更新に使い…ということができると、第1層の重みまですべてを更新することができます。
これが誤差逆伝播法という重み更新法の考え方です。
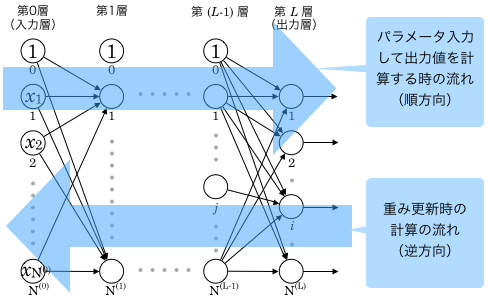
多層パーセプトロンの入力層に を入力した時は、重みを掛けながら第1層、第2層…と伝播していき、出力層から
が出力されます。
重み更新の際には、まず出力層の重み更新を計算し、その計算結果の一部を伝播させながら 第層、第
層…という “逆方向” の順番に計算していくことになります。
誤差 “逆” 伝播法 というのはそういう意味です。
重み更新は、プログラムだと出力層から順にループで処理していく形になります。
前の節で第層の更新について考えたとき、層番号以外は第
層の時とほとんど同じ形の式が現れたことを思い出してください。
これもループに適していそうですよね。
更新式の決定版は次回
ここまでは第層と第
層に注目しましたが、全ての層に適用できる更新式を導くため、任意の第
層で一般化して考えます。
長くなったのでまた次回。
-
ベクトル
と
ノルム(詳細は割愛)を使うと次のようにも書けます。
また、簡単のため、この定義はオンライン学習でベクトルを1件だけ入力した場合の誤差として記述しています。
一括学習やバッチ学習で、複数の教師データを入力して全ての誤差の和(または平均)を計算するという場合は、この誤差関数にさらにがもう1つつきます。 ↩
-
の真下に
が表示されているのと
の右下に
が表示されているのは同じ意味です。
この記事で使用している数式表示のシステムの仕様です。 ↩ - 定数倍しても相対的な大小は変わりません。 ↩
-
多層パーセプトロンの活性化関数としてステップ関数が使えない理由はこれです。
ステップ関数では微分値が0になるので、重みの更新量も0になり、つまり更新されないのです。 ↩ -
を
で偏微分したときに現れる係数
が、誤差関数の定義で付与した
と打ち消し合っているので、結果的に係数が消えてシンプルになっています。
誤差関数でをつけたのはこのためです。 ↩