今回書くこと
この記事では、特に画像識別で大きな成果を挙げた畳み込みニューラルネットワーク1の概要について書きます。
数式にはあまり触れませんので、そのあたりまで踏み込みたい方は専門の資料をご覧ください。
多層パーセプトロンで画像識別
前回までに触れた多層パーセプトロンは、画像の学習器としてはあまり強力ではありませんが、ごく小さな画像なら下記のようにすると学習できることがあります。
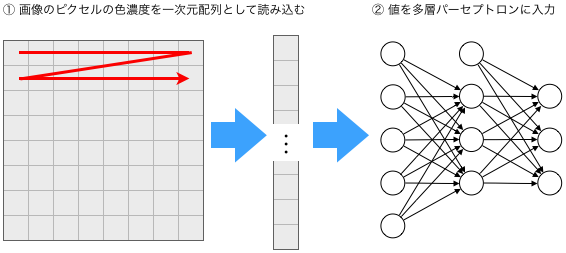
各ピクセルの色濃度を多層パーセプトロンの入力値とし、出力が正解ラベルに近づいていくように学習していきます。
ただ、この方法は2次元の画像を1次元の配列に変換しているので、例えば画像に写っているものがたった1ピクセルずれただけでも入力が大きく変わってしまいます。
これではあまり性能のいい識別器になりません。
今回説明する畳み込みニューラルネットワークという学習機械では、この問題が解決されています。
畳み込み行列による画像フィルタ
畳み込みを理解する2には、簡単な画像フィルタについて知っておくのが近道です。
ここで言うフィルタとは、画像に対して特定の演算を加えることで画像を加工するものを指します。
画像レタッチソフトに実装されているような、ぼかし・シャープ化・エッジ抽出などができます。
まず、画像の各ピクセルの色濃度を、ピクセルの並び通りに二次元に配列してみます。
(簡単のため、モノクロの画像として考えます。)

次に、画像とは別に、フィルタとなる二次元の配列を準備します。
縦横3〜11程度の小さなものを想像してください。
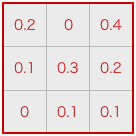
画像にフィルタをかけるとは、下記のようにして出力ピクセルを決めていく処理です。
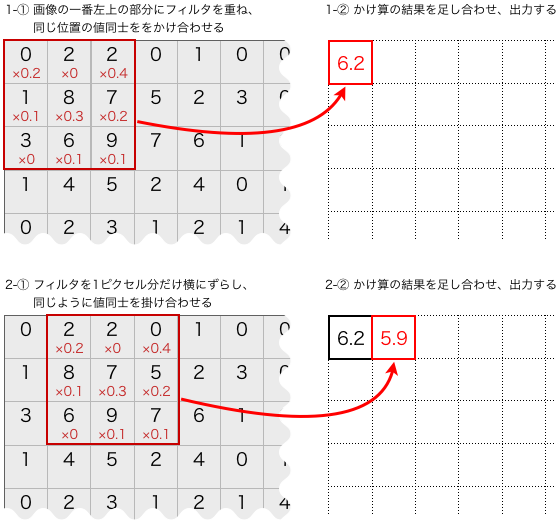
このような計算を画像の隅々まで行い、二次元配列の出力を得ます。
これで何ができるかの例として、次のようなフィルタを考えてみましょう。
(実際には、結果的に何ができるのかがわかれば十分ですので、説明文がわかりづらい場合は軽く読み流してください。)
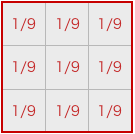
画像にこのフィルタをかけると、どうなるかわかるでしょうか?
元画像の3×3ピクセルの領域の色濃度が平均されて出力されますね。
つまり隣り合ったピクセルの色が混ざったものが出力されるわけです。
これはぼかし効果を得られるフィルタになります3。
フィルタのサイズをもっと大きくすれば、強いぼかしがかけられます。
下記のフィルタはどうでしょうか。

ゼロの部分は無視していいですね。
1と-1の部分に注目しましょう。
元の画像でこの2箇所に対応する2ピクセルが全く同じ色濃度だったら、出力値はゼロになります。
一方で、その2ピクセルの色濃度が大きく違えば、絶対値の大きな値が出力されます。
これは上下方向のエッジ(色の境界のうち、左右に走る線)の検出器として利用できます。
同じように、下記では左右方向のエッジ(色の境界のうち、上下に走る線)検出ができます。

下記はラプラシアンフィルタと言われるものの1つで、向きに関係なくエッジ検出ができるものです。

上記のようなフィルタ処理をする二次元配列を畳み込み行列といいます。
以降で「フィルタ」と言うときは、この畳み込み行列を指します。
畳み込みニューラルネットワーク
人間の脳で視覚を処理する部位は層構造を成しており、浅い(目に近い方の)層の細胞は、目で見た画像内のエッジ方向をそれぞれ検知し、深い層ではより高次の認識をするとされています。4
そういった動きを前述のようなフィルタで簡易的に再現しようという試みが畳み込みニューラルネットワークです。
前節のフィルタの説明では、畳み込み行列の各値を目的に応じてあらかじめ固定で決めておき、それを画像に適用するものとしました。
畳み込みニューラルネットワークのキモは、このようなフィルタをいくつも準備しておいて、その値を固定せず、学習によって決めていくという点にあります。
フィルタによって1ピクセルだけ出力する処理は、下記のようなものでした。
- 入力となる数値の並び(画像の一部分)がある
- この数値の並びに、それぞれフィルタの各値をかける
- かけ算の各結果をすべて足し合わせる
これ、パーセプトロンの1ノードの、下記の動きに似ていると思いませんか。
- 入力となる数値の並びがある
- この数値の並びに、それぞれ重みの各値をかける
- かけ算の各結果をすべて足し合わせる
- (活性化関数にこれを入力する)
パーセプトロンにおける学習とは、重みの値を更新していくことでした。
畳み込みニューラルネットワークでは、重みの代わりにフィルタの各値をランダムに初期化し、学習によって更新していきます。
最終的にどのようなフィルタができあがるかはデータやプログラムに任せてしまうわけです。
更新には、多層パーセプトロンと同じバックプロパゲーションを用います。
また、上記では多層パーセプトロンの説明にのみ活性化関数についての言及がありますが、畳み込みニューラルネットワークでも同じように活性化関数を適用します。
構造の概要
畳み込みニューラルネットは、層構造(多層パーセプトロンより少し複雑ですが)を持ったモデルとして表現されます。
下図に、典型的な構造の概観を示します。
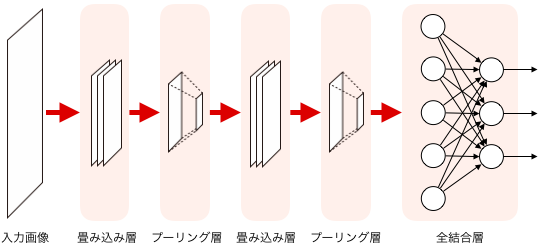
「畳み込み層」「プーリング層」と呼ばれる層が交互に2回繰り返された後、全結合層というのが配置されています。
畳み込み層とプーリング層の繰り返しは、実際にはもっと多いのが普通です。
畳み込み層は、一層で複数のフィルタを持っており、入力に対してそれらのフィルタを適用します。
結果、画像データのような二次元配列が、フィルタと同じ数だけ出力されることになります。
配列の各値には活性化関数をそれぞれ適用します。
プーリング層は、簡単に言うと畳み込み層から出力された二次元配列を縦にも横にも小さくして、有効な値だけを残すような処理をします。
これによって、元画像内でオブジェクトが多少変形していたりしても、その差異を吸収することができます。
というと難しそうですが、実はとても簡単な処理をしています。
全結合層というのは、基本的には多層パーセプトロンと同じものと思っていいです。5
最後のプーリング層が出力したデータ内のすべての値を入力します。
モデル上、この層より前の層ではデータが複数の二次元配列6の形で扱われていますが、ここで一次元配列(つまりベクトル)になり、出力層で正解ラベルと対応させることができるようになります。
入力画像に写っているのがライオンだったら出力層1番目のユニットが活性化、ペンギンだったら2番目のユニットが活性化…という具合です。
次回は、各層が実際にどのような処理をするのかを見ていきます。
- Convolutional Neural Network、略して CNN と書いたりします。 ↩
- 畳み込みという処理の一般的な(数学的な)定義はけっこう難しいので、ここでは画像における畳み込みに特化して書きます。 ↩
- 厳密には移動平均フィルタと呼ばれ、画像中の1ピクセル程度の小さなノイズを軽減するのにも使えます。 ↩
- 少し具体的に書くと、一次視覚野(V1)と呼ばれる部位のニューロンはほとんどが画像内のエッジの方向に反応することが観察されています。ある細胞は画像内の水平な線分により強く反応、別の細胞は30度傾いた線分に反応、という具合です。さらにそこからの出力を受け取るV2と呼ばれる部位の一部では、物体の角などの少し複雑な形を認識していると考えられているようです。さらに奥の部位では、見えているものが「何なのか」や、「どこにあるのか」を認識します。 ↩
- 全結合層を一層のみにする設計もあるので、その場合は「多層」とは言えませんが。 ↩
- イメージしやすいよう「複数の二次元配列」としましたが、縦サイズ・横サイズ・枚数の三次元とも考えられます。 ↩